Введение
Для того, чтобы спрогнозировать значение одной переменной на основе значения другой, или нескольких других переменных используется линейный регрессионный анализ.
Переменная, которую мы хотим предсказать, называется зависимой переменной (или регрессант).
Переменные, которые мы используем для предсказания значения зависимой переменной, называются независимыми переменными (или предикторы/регрессоры).
Модель линейной регрессии представляет собой математическую формулу, которая позволяет строить прогнозы. Построить регрессию – это значит подобрать такую линию (точнее, функцию), которая как можно точнее описывает данные.
Прежде чем подогнать линейную модель, необходимо проверить, наличие взаимосвязи между интересующими переменными.
Для определения наличия связи между переменными используют диаграмму рассеяния. Подробнее о том, почему важно визуализировать данные перед построением модели читать здесь.
Если диаграмма рассеяния показывает, что между зависимой и независимыми переменными нет связи (т. е. на графике нет возрастающих или убывающих тенденции), то подгонка модели линейной регрессии к данным, вероятно, не даст полезной модели.
Для оценки связи между двумя переменными используют коэффициент корреляции, который представляет собой значение от -1 до 1 и оценивает силу связи.
В случаях, когда есть только одна независимая переменная применяется парная (она же «простая») линейная регрессия (simple linear regression), в случаях, когда независимых переменных две и более – применяется множественная линейная регрессия (multiple linear regression).
Парная (простая) линейная регрессия
Уравнение парной линейной регрессии:
Y = b0 + b1X1 ,
где X1 — независимая переменная, а Y — зависимая переменная.
Наклон линии равен b1, а b0 — точка пересечения с осью y.
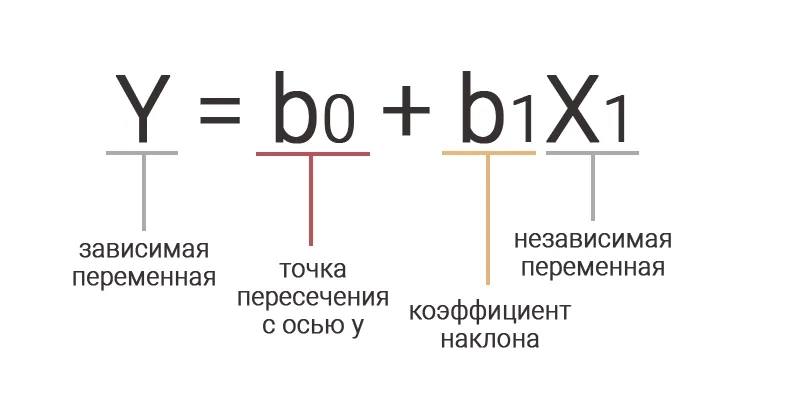
Пример парной регрессии:
y – уровень счастья кота
x – количество съеденного корма
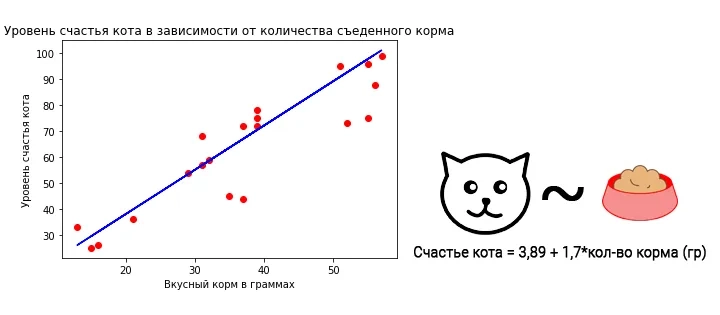
Уравнение регрессии:
Уровень счастья кота = 3,89 + 1,7*кол-во вкусного корма (гр)
b0 = 3,89 - точка пересечения оси y (если бы количество корма было 0, то прогнозируемый уровень счастья кота был бы 3,89).
b1 = 1,7 – коэффициент наклона (если увеличивать количество корма на 1 грамм, то уровень счастья кота увеличится на 1,7).
Как подобрать лучшую линию регрессии?
Наиболее распространенный метод подбора линии регрессии - метод наименьших квадратов (МНК).
МНК вычисляет наиболее подходящую линию для наблюдаемых данных путем минимизации суммы квадратов вертикальных отклонений от каждой точки данных до линии.
То есть, лучшим уравнением считается то уравнение, при котором сумма квадрата остатков сведена к минимуму: SUM(yi-ŷi)^2 -> min,
где, yi – фактическое значение, ŷi – прогнозное значение.
Множественная линейная регрессия
Уравнение множественной линейной регрессии:
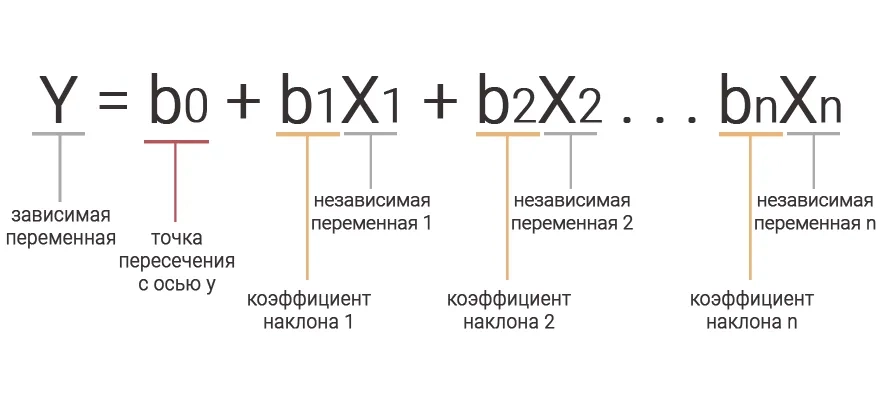
Y = b0 + b1X1 + b2X2 + … + bnXn,
где Xn — независимые переменные, а Y — зависимая переменная.
bn – коэффициент наклона для Xn , а b0 — точка пересечения с осью y.
Пример множественной регрессии:
y – уровень счастья кота
x1 – количество съеденного корма
x2 – количество поглаживаний
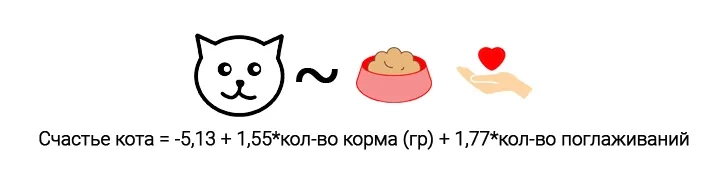
Если увеличивать количество корма на 1 грамм, то уровень счастья кота увеличится на 1,55, а если увеличивать количество поглаживаний на 1, то уровень счастья кота увеличится 1,77.
Предположения линейной регрессии
Прежде чем выполнить линейную регрессию, необходимо убедиться, что данные могут быть проанализированы с помощью этого алгоритма.
Предположения для выполнения линейной регрессии:
1. Переменные должны быть непрерывными.
Непрерывными называют переменные, которые могут принимать любое значение в определённом интервале.
2. Между переменными должна существовать линейная связь.
3. Наличие гомоскедастичности.
Гомоскедастичность – свойство, означающее постоянство дисперсии на протяжении всей линии регрессии.
4. Многомерная нормальность (нормальность распределения ошибок). Линейная регрессия предполагает, что остатки модели нормально распределены.
5. Наблюдения независимы друг от друга (мы не хотим видеть любые закономерности в наших данных).
6. Отсутствие мультиколлинеарности.
Мультиколлинеарность — явление, при котором наблюдается сильная корреляция между признаками. Мультиколлинеарность негативно влияет на модели машинного обучения.
7. Данные не должны иметь значительных выбросов.
Выброс — это наблюдение, которое лежит аномально далеко от других значений в наборе данных. Выбросы могут быть проблематичными, поскольку они могут повлиять на результаты анализа.
Применение линейной регрессии
Регрессия используется во многих областях: промышленность, здравоохранение, научные исследования, финансы, маркетинг и прочее. Модели линейной регрессии считаются проверенным способом научного и надежного прогнозирования будущего.
Например, производственные компании используют регрессионный анализ для оценки вероятности выхода из строя деталей оборудования.
Медицинские исследователи используют регрессионные модели для прогноза вероятности заболевания у пациентов.
Финансовые компании используют регрессионный анализ для оценки финансовых рисков, оценки платежеспособности клиентов.
Маркетинговые компании оценивают потенциал клиентов на будущие периоды, владея некоторой информацией о клиенте: пол, возраст, доход.
Помощь в построении прогностических моделей
Необходимо построить прогнозную модель, которая по значению некоторого набора известных данных будет определять значение неизвестного показателя?
Мы можем Вам помочь!
- Подберем корректные методы обработки и анализа данных
- Преобразуем данные в удобный для анализа вид
- Проведем необходимые вычисления, построим прогнозную модель
- Опишем и оформим результаты: выводы, таблицы, графики.
Проведем быстрый и качественный статистический анализ данных!
Оказываем быструю и качественную помощь в статистических расчетах для научных статей, диссертаций или маркетинговых исследований.
Свяжитесь с нами одним из удобных способов, чтобы обсудить детали:
WhatsApp: +7 (919) 882-93-67
Telegram: birdyx_ru
E-mail: mail@birdyx.ru